L’Axiome du Choix : Comment une Règle Simple a Créé les Paradoxes les Plus Troublants des Mathématiques

Il existe une règle en mathématiques qui est si simple que l’on pourrait penser qu’elle doit évidemment être vraie, mais si on l’accepte, on découvre qu’il y a maintenant des segments de ligne qui n’ont aucune longueur. Une sphère sans rien y ajouter peut être transformée en deux sphères identiques. Plus de cent ans de mathématiques ont été construites sur cet axiome. Il semble intuitif et il fonctionne, mais il crée aussi des paradoxes ridicules. Alors, est-il correct ?

Eh bien, tout commence avec la question du choix.

Le Problème Fondamental du Choix en Mathématiques

Essayez ceci : choisissez un nombre. Je peux simplement extraire un nombre aléatoire de ma tête, comme 37 ou 42, mais c’est le cerveau humain à l’œuvre, pas un processus mathématique. En mathématiques, on ne peut pas vraiment choisir des choses au hasard parce que les formules donnent toujours le même résultat, c’est pourquoi les ordinateurs n’ont pas de vrais générateurs de nombres aléatoires. Au lieu de cela, ils exécutent généralement un algorithme sur votre heure locale actuelle pour générer des nombres qui semblent aléatoires.

Donc si nous ne pouvons pas choisir au hasard, comment sélectionnons-nous quoi que ce soit en mathématiques ? Eh bien, la seule façon est de suivre une règle quelconque. Donc une règle pourrait être de toujours choisir la plus petite chose. Par exemple, si nous regardons les entiers positifs entiers, le plus petit est un.

Pour les nombres premiers, ce serait deux, facile, mais qu’en est-il des nombres réels ?

L’Impossibilité de Choisir le Plus Petit Nombre Réel

C’est n’importe quel nombre, positif, négatif, entier, fraction, même irrationnel comme pi ou la racine carrée de deux. Maintenant, essayez de choisir le plus petit. C’est impossible. Les nombres réels s’étendent jusqu’à l’infini négatif. Même si nous essayons de corriger notre règle en la rendant super spécifique, comme choisir le plus petit nombre après un, nous restons bloqués. Il y a 1,01 et puis 1,0001, puis 1,00000000001 et ainsi de suite. Alors vraiment, quel nombre vient après un ?

Si nous ne pouvons pas commencer à spécifier l’ordre des nombres réels, suivant et précédent, premier et dernier, nous sommes bloqués. La partie ridicule est que nous savons que nous avons des options infinies, mais malgré cela, nous ne pouvons pas comprendre comment en choisir une seule.

La mission pour résoudre cela a commencé avec un homme en 1870. Il a pris sur lui la tâche de mettre les nombres réels dans un ordre définitif, même si cela le tuait et cela a failli le faire.

Georg Cantor : L’Homme qui Défia l’Infini

Georg Cantor était un mathématicien allemand talentueux qui s’est retrouvé au centre d’une tempête de feu après avoir publié l’un de ses tout premiers articles à l’âge de 29 ans. Pendant des siècles, notre compréhension de l’infini était fortement influencée par le livre de Galilée de 1638. Il soulevait une question clé : y a-t-il plus de nombres naturels ou y a-t-il plus de nombres carrés ?

En les regardant simplement, les nombres carrés sont plus espacés et ils ne deviennent que plus clairsemés plus on monte. Donc il semblerait qu’il y ait moins de carrés que de nombres naturels, mais Galilée a réalisé qu’il pouvait tracer une ligne associant chaque nombre naturel avec son propre carré. Et puisqu’il pouvait faire cette correspondance un-à-un, il savait que les deux ensembles devaient être exactement de la même taille. Donc il y a en fait autant de nombres carrés qu’il y a de nombres naturels.

De ce résultat contre-intuitif, Galilée a conclu que des termes comme “plus que” ou “moins que” ne s’appliquent pas à l’infini, comme nous les utilisons normalement. C’est tout simplement un grand concept d’éternité et cette vision a prévalu pendant des siècles. En fait, c’est comme ça que beaucoup de gens comprennent encore l’infini aujourd’hui, mais 200 ans plus tard, Cantor n’était pas satisfait.

En 1874, il s’est demandé : et s’il y avait deux ensembles infinis là-bas qui ne se correspondaient pas parfaitement l’un à l’autre ? Seraient-ils des infinis différents ? Donc il s’est mis à comparer les nombres naturels et les nombres réels entre zéro et un.

La Preuve de Diagonalisation : Il Existe Différentes Tailles d’Infini

Cantor a commencé en supposant qu’il pouvait parfaitement faire correspondre ces ensembles l’un à l’autre, un-à-un. Donc il a imaginé écrire une liste infinie avec un nombre naturel d’un côté et un nombre réel entre zéro et un de l’autre. Puisqu’il n’y a pas de plus petit nombre réel, il les écrirait simplement dans n’importe quel ordre.

En supposant qu’il a maintenant une liste infinie complète, Cantor écrit un autre nombre réel et pour le faire, il prend le premier chiffre du premier nombre et ajoute un, puis le deuxième chiffre du deuxième nombre, et encore, il ajoute un. Il continue à faire cela tout le long de la liste. Si le chiffre est un huit ou un neuf, il soustrait un au lieu d’ajouter pour éviter les doublons, et à la fin de ce processus, il a écrit un nombre réel entre zéro et un, mais ce nombre n’apparaît nulle part dans sa liste.

Il est différent du premier nombre à la première place décimale, différent du deuxième nombre à la deuxième place décimale et ainsi de suite. Il doit être différent de chaque nombre de la liste d’au moins un chiffre, le chiffre sur la diagonale. C’est pourquoi cela s’appelle la Preuve de Diagonalisation de Cantor et elle montre qu’il doit y avoir plus de nombres réels entre zéro et un qu’il n’y a de nombres naturels s’étendant à l’infini.

Le Théorème du Bon Ordre : Une Quête Apparemment Impossible

Cantor avait révélé quelque chose de remarquable. L’infini ne vient pas en une seule taille. Certains infinis comme l’ensemble des nombres carrés, des entiers ou des nombres rationnels peuvent être parfaitement appariés avec les nombres naturels. Vous pouvez littéralement les compter, un, deux, trois et ainsi de suite. Donc Cantor a appelé ces infinis dénombrables, mais alors il y a de plus grands infinis, Cantor les a appelés indénombrables. Ces infinis comme l’ensemble de tous les nombres réels, les nombres complexes, ils ne peuvent pas être appariés un-à-un avec les nombres naturels.

Les résultats de Cantor ont secoué la communauté mathématique. Après tout, comment quelque chose qui continue pour toujours peut-il être plus grand que quelque chose d’autre qui continue pour toujours ? Son travail a été qualifié d’horreur et de maladie grave, mais Cantor n’était pas découragé. Son succès n’a fait que l’inciter à poursuivre son objectif encore plus grandiose de montrer que même les ensembles infiniment indénombrables pouvaient être placés dans un ordre définitif. Ce que Cantor appelait un bon ordre.

Pour qu’un ensemble soit bien ordonné, il exigeait deux conditions. Premièrement, l’ensemble doit avoir un point de départ clair. Et deuxièmement, chaque sous-ensemble, une collection d’éléments de cet ensemble, doit aussi avoir un point de départ clair. Donc par exemple, les nombres naturels sont bien ordonnés, il y a un point de départ, un, et tout sous-ensemble, disons six, sept, huit, a aussi un point de départ clair. Dans ce cas, six, vous savez toujours quel nombre vient avant et lequel vient après.

Mais qu’en est-il des entiers ? Les entiers s’étendent à l’infini dans les directions positive et négative. Eh bien, Cantor a réalisé qu’il pouvait simplement choisir zéro comme point de départ et de là son classement était un, moins un, deux, moins deux, classant les entiers par leur valeur absolue, leur distance de zéro. Peu importe si vous mettez les positifs en premier ou les négatifs en premier, tant que vous êtes cohérent.

Les ordonner de cette façon est en fait ce qui nous permet de faire correspondre les entiers aux nombres naturels et de voir que les deux ensembles sont de la même taille, mais il y a d’autres façons dont nous pourrions bien ordonner les entiers. Nous pourrions commencer avec zéro et puis avoir un, deux, trois, tout le chemin jusqu’à l’infini positif et puis moins un, moins deux, moins trois, tout le chemin jusqu’à l’infini négatif. Ce n’est pas comme ça que nous avons l’habitude de compter, mais ces deux options correspondent à la définition d’un bon ordre. Il y a un point de départ clair, zéro, et tous leurs sous-ensembles ont aussi un point de départ définitif.

Cantor avait réussi à bien ordonner un ensemble qui était infini dans les deux directions, mais il n’était que dénombrablement infini. Dans son livre suivant, il a publié son théorème du bon ordre. Il prétendait que chaque ensemble, même les indénombrablement infinis comme les nombres réels pouvaient être bien ordonnés. Le problème était qu’il n’avait pas réellement prouvé cela parce qu’il ne pouvait pas, chaque méthode qu’il essayait avait échoué, mais il y avait une grande raison pour laquelle Cantor était si confiant dans son théorème.

La chute et la Persécution de Cantor

Cantor était un luthérien dévot et il croyait que Dieu parlait à travers lui. Il a dit : “Ma théorie se dresse ferme comme un roc. Chaque flèche dirigée contre elle retournera rapidement à son archer. Comment je le sais ? Parce que je l’ai étudiée sous tous les angles pendant de nombreuses années et surtout parce que j’ai suivi ses racines pour ainsi dire, jusqu’à la première cause infaillible de toutes les choses créées.”

Croyance mise à part, le théorème du bon ordre était une affirmation audacieuse à faire sans aucune preuve mathématique. Et donc pour la deuxième fois, la communauté mathématique a attaqué et ostracisé Cantor. Menant la charge était Leopold Kronecker, le chef des mathématiques à l’Université de Berlin. Kronecker a complètement rejeté le travail de Cantor, l’étiquetant comme un charlatan scientifique et un corrupteur de la jeunesse. Et Kronecker était l’ancien professeur de Cantor.

Cantor rêvait de le rejoindre à l’Université de Berlin, mais toutes ses candidatures étaient mystérieusement refusées. Donc Cantor a pris le rejet personnellement. En 1884, il a écrit 52 lettres à un ami et chacune d’elles déplorait Kronecker. Bientôt Cantor a souffert de ce qui serait la première de nombreuses dépressions nerveuses. Il a été confiné dans un sanatorium pour récupérer. La seule façon qu’il pouvait prouver que tout le monde avait tort était en ordonnant bien les nombres réels, mais il ne pouvait pas trouver un point de départ, littéralement.

Une fois que Cantor a été libéré du sanatorium, il s’est éloigné des mathématiques, un homme brisé. Et au cours des 15 années suivantes, il a enseigné la philosophie et s’est rarement penché sur ses anciennes poursuites. Peut-être que son plus grand défi est venu au Congrès international des mathématiciens de 1904. Là, Julius König, un professeur respecté de Budapest, a annoncé qu’il avait la preuve que le théorème du bon ordre de Cantor était faux.

Dans l’audience se trouvait non seulement Cantor mais aussi sa femme, deux de ses filles et ses collègues. Il se sentait complètement humilié, mais il y avait aussi un autre présent. Ernst Zermelo.

Ernst Zermelo : Le Sauveur Inattendu

Zermelo était un mathématicien allemand qui avait récemment développé un vif intérêt pour le travail de Cantor et en écoutant la présentation de König, quelque chose semblait incorrect. En 24 heures, Zermelo avait identifié le problème. La preuve de König contenait une contradiction accablante, et en un mois, Zermelo a publié un article de trois pages intitulé “Preuve que chaque ensemble peut être bien ordonné” et il était impeccable.

La percée de Zermelo est venue quand il a découvert quelque chose de profond dans le travail de Cantor, un mécanisme que Cantor utilise inconsciemment et instinctivement partout, mais ne formule explicitement nulle part. Voyez, tout le temps, Cantor avait supposé qu’il pouvait faire un nombre infini de choix à la fois de n’importe quel ensemble, y compris des ensembles infiniment indénombrables comme les nombres réels, mais c’était juste une supposition. Nulle part dans le livre de règles mathématiques cela n’était explicitement permis et les mathématiques sont construites sur des règles, spécifiquement des axiomes.

Les axiomes sont des déclarations simples que nous acceptons comme vraies sans preuve. Zermelo a réalisé que la supposition de Cantor devait être formalisée en quelque chose qui tient dans un système de preuve. Un nouvel axiome qui disait que faire tous ces choix était possible. Il avait besoin de l’axiome du choix.

L’Axiome du Choix : Formaliser l’Impossible

L’axiome du choix peut être dit dans le sens que si vous avez infiniment de nombreux ensembles et chaque ensemble n’est pas vide, alors il y a un moyen de choisir un élément de chacun des ensembles.

Pour les ensembles finis, cela semble évident, juste aller ensemble par ensemble et choisir quelque chose. Même pour les ensembles infinis, c’est facile s’il y a une règle claire, comme toujours choisir la plus petite chose, mais parfois il n’y a pas de règle naturelle. Dans ces cas quand vous choisissez parmi infiniment de nombreux ensembles, y compris les indénombrables, vous avez besoin de l’axiome du choix. Nous ne pouvons pas dire comment nous choisissons, mais l’axiome fait tous ces choix en même temps.

L’axiome ne vous permet pas de dire quel élément vous avez choisi, seulement qu’infiniment de nombreux choix sont possibles. Donc comment ce nouvel axiome nous permet-il de bien ordonner les nombres réels ?

Comment Bien Ordonner les Nombres Réels

Zermelo utilise l’axiome du choix pour choisir un nombre de l’ensemble de tous les nombres réels. Il place ce nombre, appelons-le X1 dans un nouvel ensemble, R. L’axiome lui permet alors de choisir un autre nombre du sous-ensemble de tous les réels moins celui retiré. Il appelle ce nombre X2 et le place comme le nombre suivant dans son ensemble et il continue à faire cela, prenant le nombre choisi et le plaçant suivant, X3, X4, X5.

Maintenant, il semble qu’il choisisse ces nombres un à la fois, mais en réalité les choix sont faits de tous les sous-ensembles possibles en même temps. Comme Zermelo indexe chaque nombre avec les nombres naturels, au début il pourrait sembler qu’il rencontrerait un problème parce que les nombres naturels ne sont que dénombrablement infinis, alors qu’il y a beaucoup plus de réels. Donc il devrait finalement manquer d’étiquettes, mais nous pouvons compter au-delà de l’infini.

Nous l’avons fait plus tôt quand nous avons compté au-delà de l’infini positif pour arriver à moins un, moins deux et ainsi de suite. Donc nous avons juste besoin d’un nouvel ensemble de nombres qui s’étend au-delà des naturels, appelons le nombre suivant oméga, puis oméga plus un, oméga plus deux, et ainsi de suite. Ces nombres oméga ne sont pas plus grands que l’infini. Ils viennent juste après l’infini. Ils ne nous disent pas combien de choses il y a, mais ils nous disent leur ordre.

Donc le nombre suivant que nous sortons, nous l’étiqueterons X oméga, puis X oméga plus un, X oméga plus deux, et ainsi de suite. Cela continuera jusqu’à ce que nous égalions la taille des nombres réels et notre ensemble original soit vide. Maintenant, chaque nombre réel est dans notre nouvel ensemble. Il y a un premier nombre, X1, et chaque sous-ensemble a aussi un premier nombre. Et comme ça, nous avons réussi à bien ordonner les nombres réels.

Cet ordre ne ressemble en rien à notre ordre familier. Un milliard pourrait venir avant 0,2, mais avec ce processus, nous pouvons prouver qu’un bon ordre existe. Et plus que cela, nous avons maintenant un moyen de résoudre notre problème de comment choisir mathématiquement. Nous ne pouvons pas choisir un plus petit nombre réel, mais maintenant nous pouvons choisir un premier nombre réel, notre point de départ, et nous pouvons faire cela pour n’importe quel ensemble, signifiant que tous les ensembles peuvent être bien ordonnés peu importe l’infini.

Donc le théorème du bon ordre de Cantor et l’axiome du choix de Zermelo sont équivalents. Cantor était si soulagé. Zermelo avait prouvé le théorème du bon ordre et bien ordonné les nombres réels tout en moins d’un mois. Zermelo a pris quelque chose sur quoi les mathématiciens s’appuyaient inconsciemment depuis des décennies et l’a transformé en un axiome formel. Il a montré que comprendre les mathématiques ne concerne pas seulement les nombres, c’est la logique derrière eux.

---

L’axiome du choix était peut-être une nouvelle idée, mais son utilisation était tout sauf. Zermelo a scanné des dizaines d’articles d’autres mathématiciens et a réalisé qu’ils avaient aussi utilisé l’axiome tout le temps, même ceux qui avaient critiqué le travail de Cantor.

Cela montre juste à quel point c’est peu intuitif que c’est même un axiome. Les gens l’avaient utilisé pendant comme une décennie, inconsciemment.

Mais cela semble presque trop évident. La preuve de Zermelo n’a pas réellement construit un bon ordre. Elle a juste dit qu’un doit exister, mais quelque chose peut-il exister si nous ne pouvons pas réellement le construire ? Sa preuve a aussi utilisé un nombre indénombrable d’étapes, était-ce même permis ? Certains mathématiciens ont argumenté que les preuves devraient être finies, d’autres ont accepté l’infini, mais seulement le type dénombrable et puis les choses ont empiré.

Les Conséquences Troublantes : L’Ensemble de Vitali

Quand les mathématiciens ont joué avec l’axiome du choix, cela a créé des résultats troublants. L’un des premiers est venu de Giuseppe Vitali en 1905. Vitali a utilisé l’axiome du choix pour construire un ensemble de nombres qui a brisé notre idée de ce que cela signifie pour quelque chose d’avoir une longueur.

Donc ce que fait Vitali c’est qu’il prend chaque nombre réel entre zéro et un et l’assigne à l’un d’un nombre infini de bacs. Appelons ces bacs des groupes. Donc nous voulons que chaque nombre réel finisse dans exactement l’un de nos bacs infinis. Donc comment fait-il cela ?

Eh bien, disons que nous avons deux nombres, X et Y. Si leur différence, X moins Y est égale à un rationnel, c’est-à-dire un entier divisé par un autre entier, eh bien alors X et Y iront dans le même bac. Mais si nous avons deux autres nombres, disons P et Q et leur différence n’est pas un rationnel, donc c’est une différence irrationnelle, eh bien alors ces deux nombres iront dans des bacs séparés.

Donc faisons quelques exemples. Si c’est 3/4 moins un demi, alors nous obtenons un quart et donc 3/4 et un demi iront dans le même bac. En fait, vous pouvez voir que tous les nombres rationnels de cette étendue, zéro à un, ils finiront tous dans le même groupe.

Maintenant si vous avez des nombres irrationnels, eh bien ce n’est pas clair s’ils iront dans le même bac ou pas parce que par exemple, si nous avons le nombre racine deux sur deux moins disons racine deux sur deux moins un quart, eh bien alors cela a une différence rationnelle même si chacun de ces nombres est irrationnel. Donc ces deux nombres iront dans le même groupe, mais si nous avons des nombres irrationnels racine deux sur deux moins racine deux sur trois, eh bien cela donne une différence irrationnelle. Donc racine deux sur trois devra aller dans un bac différent et il sera rejoint par tous les nombres avec lesquels il a une différence rationnelle.

Et de cette façon, vous pouvez assigner chaque nombre réel à exactement l’un de ces bacs. Ensuite, Vitali a utilisé l’axiome du choix pour atteindre dans chaque groupe et sélectionner exactement un nombre, qui serait un représentant du groupe. Donc nous pourrions sortir 3/4 du groupe rationnel, racine deux sur deux de ce groupe, racine deux sur trois de ce groupe et ainsi de suite. Bien sûr, parce que nous utilisons l’axiome du choix, vous ne savez pas réellement quel est ce nombre représentant, juste que vous en avez un.

Donc nous pourrions l’écrire comme ceci. Nous avons ces représentants de chaque groupe et ensemble ils forment l’ensemble de Vitali. Vous pouvez visualiser cet ensemble comme une collection de points entre zéro et un. Ensuite, Vitali fait des copies infinies de son ensemble et chacune il la décale par un nombre rationnel différent entre moins un et plus un.

Donc si vous pensez à ce que cela fait, cela va déplacer chaque nombre représentant pour être à la position de chaque autre nombre dans son groupe. Si nous avions juste le seul nombre rationnel que nous avons extrait comme représentant du groupe rationnel, maintenant nous allons le décaler par chaque nombre rationnel possible entre moins un et plus un. Donc il va finir à chaque autre position occupée par les autres membres de son groupe, au moins sur l’étendue entre zéro et un.

Donc si vous imaginez maintenant fusionner tous ces ensembles infinis ensemble, il n’y aura pas de chevauchement entre les points. Et deuxièmement, nous allons avoir chaque nombre réel entre zéro et un parce que sur cette étendue nous avons chaque membre de chaque groupe.

Donc maintenant la question est quelle est la taille de l’ensemble de Vitali ? Maintenant nous savons que l’union de ces ensembles doit être supérieure ou égale à un parce que nous avons chaque nombre réel entre zéro et un, mais aussi ces points s’étendent seulement jusqu’à moins un ou plus deux. Donc cela doit être inférieur ou égal à trois, mais c’est là que le problème surgit parce que quel nombre pour la taille de l’ensemble de Vitali pourriez-vous ajouter à lui-même infiniment de nombreuses fois et finir avec une valeur entre un et trois ?

Il n’y a pas de nombre comme ça. Je veux dire si la taille de l’ensemble de Vitali était zéro, vous l’ajoutez infiniment de nombreuses fois vous obtenez encore zéro. Si la taille de l’ensemble de Vitali est une petite valeur positive, alors vous l’ajoutez infiniment de nombreuses fois, vous allez obtenir l’infini, pas trois. Donc nous avons une contradiction et la seule sortie est si l’ensemble de Vitali lui-même est non mesurable, ce qui semble fou.

Les ensembles non mesurables comme l’ensemble de Vitali n’ont pas de définition cohérente de taille ou longueur ou aire ou même probabilité. Mais les mathématiques sont construites sur l’idée que tout peut être quantifié, que ce soit la distance, le temps, ou le poids, sauf maintenant il y a des ensembles non mesurables et il semble que l’axiome du choix soit à blâmer.

Le Paradoxe de Banach-Tarski : Doubler une Sphère par Magie

C’était juste le début du tollé causé par l’axiome. En 1924, deux mathématiciens, Stefan Banach et Alfred Tarski l’ont utilisé pour montrer quelque chose qui ressemble à un tour de magie. Ils ont prouvé que vous pourriez prendre une seule balle solide et la diviser en juste cinq pièces, et puis en faisant tourner et bougeant soigneusement ces pièces, vous pourriez les rassembler en deux balles chacune identique à celle avec laquelle nous avons commencé, et vous pourriez continuer jusqu’à finalement avoir un nombre infini de balles, l’infini tout d’une seule.

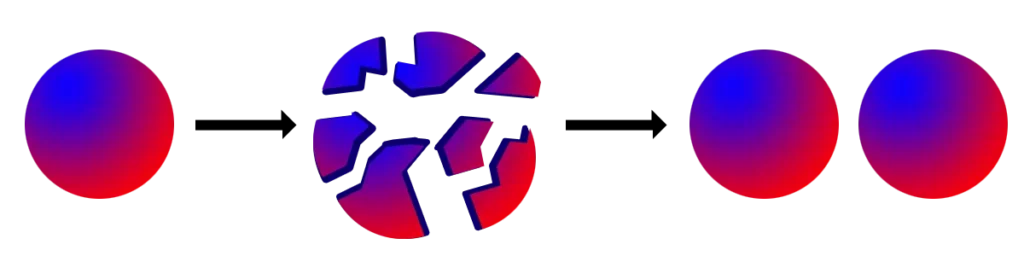
Cela semble absurde, mais nous pouvons réellement voir comment cela fonctionne en construisant un graphique. Imaginez que vous pouvez vous déplacer dans quatre directions, haut, bas, gauche et droite. Après avoir fait un pas, disons vers la gauche, vous obtenez les mêmes quatre choix, haut, bas, gauche et droite, mais si vous allez à droite, vous finirez de retour où vous avez commencé. Donc la seule règle que nous allons avoir est que vous ne pouvez pas immédiatement inverser un mouvement, et nous continuerons à répéter cela à chaque étape, dessinant chaque nouvelle ligne, la moitié de la taille de la précédente pour que tout rentre sur l’écran.

Si nous continuons, nous finirons avec ce graphique infiniment ramifié. En regardant notre graphique, nous pouvons le diviser en cinq sections. Il y a la section du milieu où nous avons commencé, et puis il y a quatre autres sections qui sont toutes identiques, juste tournées. Donc si nous prenons cette section à gauche et nous déplaçons tout d’un pas vers la droite, la partie du haut finit ici, la partie du bas ici, et la partie la plus à gauche ici, alors nous avons presque recréé le graphique entier. La seule chose qui nous manque est cette section, donc ajoutons-la de retour, mais nous aurions pu faire la même chose d’une façon complètement différente en prenant la section du bas et en la déplaçant d’un pas vers le haut.

Maintenant la partie la plus à gauche finit ici, la partie la plus à droite ici et le bas ici. Encore, nous manquons juste une section, donc ajoutons-la de retour. Mais cela signifie que je peux recréer le graphique original entier de deux façons complètement différentes. Nous avons pris un graphique, l’avons divisé en sections, avons décalé les sections, donc la section de gauche est allée à droite et la section du bas vers le haut et avons en quelque sorte fini avec deux copies identiques.

C’est exactement ce que Banach et Tarski ont fait, mais avec une balle, comme notre graphique, nous avons encore quatre mouvements. Nous pouvons faire tourner la balle vers le haut, le bas, la gauche ou la droite, et encore, notre seule règle est que nous ne pouvons pas immédiatement inverser un mouvement. Et pour s’assurer que nous ne revenons jamais au même point, chaque rotation sera par la même portion irrationnelle d’un cercle.

Nous pouvons choisir un point de départ aléatoire, le marquer et puis commencer à faire tourner la balle. Chaque point est coloré basé sur la direction de rotation utilisée pour y arriver. Si nous faisons cela un nombre infini de fois, nous finissons avec cette collection de points. C’est une collection dénombrablement infinie parce que nous pourrions lister chaque rotation et lui assigner un nombre naturel, mais la surface d’une balle a des points indénombrablement infinis juste comme la ligne des nombres réels.

Donc si nous voulons couvrir la surface entière, nous devrions répéter ce processus, mais où commençons-nous ensuite ? Puisqu’il y a des points de départ indénombrablement infinis possibles, nous ne pouvons pas tous les lister et nous voulons être sûrs d’éviter tous les points que nous avons déjà colorés. Donc la solution est d’utiliser l’axiome du choix.

Avec lui, nous pouvons choisir des points de départ uniques, même si nous ne pouvons pas dire exactement comment nous les choisissons. Une fois que nous avons coloré chaque point sur la balle, nous pouvons diviser les points en cinq groupes, un pour les points de départ et quatre autres basés sur la rotation finale utilisée pour arriver à ces points. Ces groupes peuvent maintenant être traités juste comme les sections de notre graphique.

Nous pouvons prendre le groupe de points qui se termine avec une rotation à gauche et le faire tourner vers la droite. Puis nous ajoutons le groupe qui se termine avec une rotation à droite, et comme ça, nous avons recréé notre balle originale et nous pouvons le refaire en faisant un mouvement supplémentaire pour tenir compte des points de départ.

Nous pouvons également prendre le groupe qui se termine avec une rotation vers le bas et le faire tourner vers le haut. Puis nous ajoutons le groupe qui se termine avec une rotation vers le haut et nos points de départ, et maintenant nous avons recréé notre balle originale une deuxième fois.

Maintenant, c’est un peu une simplification excessive, mais cela vous donne l’essence de comment cela se fait. D’une balle, nous avons créé deux balles identiques du même volume, et rien ne nous empêche de refaire cela. Deux balles peuvent devenir quatre, quatre deviennent huit, et avant que vous le sachiez, vous avez des balles infinies.

L’axiome du choix est quelque chose qui est si évidemment vrai et ses conséquences sont si évidemment fausses que vous êtes comme, qu’est-ce qui se passe ?

Cette duplication infinie est théoriquement possible, mais le piège est que les groupes en lesquels nous divisons la balle ne sont pas des formes simples. Ils sont en fait non mesurables, juste comme l’ensemble de Vitali, bien que la balle originale ait un volume et les balles dupliquées aient un volume, l’étape entre viole notre compréhension de la taille. C’est ce qui permet au paradoxe de se produire.

Bien sûr, ce ne sont pas des coupes physiquement plausibles, mais il y a une question plus métaphysique comme, cela devrait-il même être à distance possible si nous pouvions faire de telles coupes ? Et la réponse à presque chaque humain que je connais est absolument pas.

La vérité est que personne ne savait ce qui se passait. Cette même année, Tarski a essayé de pousser l’axiome du choix plus loin en prouvant qu’il est équivalent à la déclaration que mettre au carré n’importe quel ensemble infini n’augmenterait pas sa taille. Quand Tarski a d’abord soumis ce travail à un journal à Paris, l’éditeur Lebesgue a répondu avec mépris, personne n’est intéressé par l’équivalence entre deux déclarations fausses. Non découragé, Tarski l’a envoyé à un éditeur différent au même journal, Fréchet, sa réponse, personne n’est intéressé par l’équivalence de deux déclarations évidemment vraies. Tarski n’a plus jamais soumis un article là-bas.

Trente Années de Crise Mathématique

Donc les mathématiques étaient en crise pendant plus de 30 ans avec des gens ne sachant pas quoi croire.

La question est, attendez une seconde, est-ce vraiment un axiome ou est-ce quelque chose que vous pouvez prouver ?

En 1938, nous avons finalement commencé à obtenir quelques réponses. Le mathématicien autrichien, Kurt Gödel, a prouvé qu’il y a un monde où tous les autres axiomes déjà acceptés de la théorie des ensembles sont vrais, et l’axiome du choix aussi. Puis en 1963, Paul Cohen a prouvé qu’il y a aussi un monde où tous les axiomes de la théorie des ensembles sont vrais sauf l’axiome du choix.

C’est un peu comme le postulat parallèle en géométrie. Vous pouvez penser à la géométrie comme un jeu. Les quatre premiers postulats ou axiomes sont comme les règles minimales requises pour jouer ce jeu, et puis le cinquième axiome sélectionne l’univers dans lequel vous voulez jouer. Si vous choisissez que le cinquième axiome ne tient pas, donc il n’y a pas de lignes parallèles, alors vous jouez en géométrie sphérique. Si vous choisissez une ligne parallèle, vous jouez en géométrie plate, et si vous choisissez plus d’une ligne parallèle, alors vous jouez en géométrie hyperbolique.

Toutes ces géométries sont valides. Cela dépend juste des mathématiques que vous voulez faire, et c’est pareil pour l’axiome du choix. L’axiome du choix ne peut ni être prouvé ni être réfuté à partir des autres axiomes. Donc tant que les autres axiomes sont cohérents, ajouter le choix ne mènera à aucune contradiction.

Paul Cohen a reçu la Médaille Fields trois ans plus tard pour son résultat révolutionnaire, ainsi que son autre travail en théorie des ensembles, et après le travail de Gödel et Cohen, la plupart des débats sur l’axiome du choix se sont calmés.

À la fin, ce qui se passe c’est que c’est à vous de décider si vous voulez choisir que l’axiome du choix fasse partie de votre système ou pas, et faire face aux conséquences soit de l’avoir soit de ne pas l’avoir.

L’Acceptation Moderne : Pourquoi l’Axiome du Choix Triomphe

Malgré les résultats contre-intuitifs créés par l’axiome du choix, comme les ensembles non mesurables et la duplication infinie, il est incroyablement utile, le choix permet aux mathématiciens de remplacer de longues preuves explicites par des arguments plus concis. En prouvant des déclarations dans le cas fini, beaucoup de preuves peuvent être étendues à n’importe quel cas infini en juste une ligne. Cela réduit des preuves qui auraient pu être de 20 pages à juste une demi-page.

Et l’axiome du choix ne rend pas seulement les mathématiques plus faciles. Il est essentiel à certaines preuves. Il y a beaucoup de théorèmes où le cas général ne peut pas être prouvé sans utiliser le choix quelque part. Maintenant, certains mathématiciens préfèrent encore les preuves sans choix, même si c’est plus difficile, la preuve doit être épelée étape par étape pour généraliser aux cas infinis, et cela fournit des informations supplémentaires.

Certains mathématiciens passent leur temps à étudier des univers sans l’axiome du choix pour comprendre ce qui se passe quand nous l’enlevons. Mais aujourd’hui, l’axiome du choix est presque universellement accepté. Pendant les 80 dernières années et plus, des générations de mathématiciens ont été enseignées avec le choix comme donné au point où beaucoup qui utilisent l’axiome du choix pourraient même ne pas réaliser quand ils le font.

Si vous n’incluez pas l’axiome du choix, alors vous travaillez en quelque sorte avec les deux mains liées derrière le dos. Il est très difficile de faire des progrès en mathématiques modernes.

Donc la question n’était jamais vraiment : l’axiome du choix est-il correct ? Mais plutôt : l’axiome du choix est-il correct pour ce que vous voulez faire ?